Learn About Randomization
As defined by the NIH, clinical trials are research studies in which "subjects are prospectively assigned to one or more interventions (which may include placebo or other control) to evaluate the effects of those interventions on health-related biomedical or behavioral outcomes."
Interventions must be evaluated impartially and without bias; otherwise, the trial results will be thrown into question. The first step in reducing bias is to assign participants to interventions (into treatment arms) in a fair manner, not influenced by an anticipated result of the intervention, such as a favorable response to treatment. The assignment to treatment arm should be as unpredictable as possible, and we attain this desired lack of prediction through a process known as randomization.
Not all randomization procedures are equally random. Unfortunately, some researchers employ less ideal, more predictable procedures because they are not aware that better randomization methods are available.
This site is intended to promote randomization procedures which reduce assignment predictability, and thus limit the potential for selection bias, while also guaranteeing balanced allocation to the available interventions.
Reducing predictability with randomization
To ensure an unbiased treatment comparison, the treatment arms must consist of participants with similar characteristics. To avoid selection bias, we must ensure that participants are not assigned to an arm based on identifiable health characteristics. [1] To this end, participants are assigned to arms randomly. All randomization procedures are intended to reduce selection bias, but they differ in how effectively they achieve this goal. Therefore, the method of randomization chosen must aim to reduce the predictability of assignment to each treatment arm.

Maintaining balance over time
According to a trial's design, each treatment arm will have been assigned a certain number of participants by each time point. Ideally the arms will maintain balance throughout the randomization process. [2] However, if treatment arms are assigned randomly without restriction, the arms may become too imbalanced, potentially leading to issues such as chronological bias (see Unrestricted Randomization below). The method of randomization chosen must ensure that, as the randomization proceeds, the expected number of participants are assigned to each treatment arm and that balance is maintained over time.
A maximum tolerated imbalance (MTI) procedure is an ideal way to randomly assign participants to treatment arms in a clinical trial. As the name suggests, MTI procedures guide the randomization by limiting the difference in the arms' counts at each point in time. Therefore, as each participant is recruited, the difference between the numbers of participants randomized to any two treatment arms never exceeds this limit, the MTI value.
While some randomization procedures maintain balance across treatment arms, MTI procedures have an important advantage when compared to other methods. MTI procedures maintain arm balance with reduced predictability of arm assignment. This is a crucial consideration, as the ability to predict upcoming treatment arm assignments must be minimized.
Example of MTI randomization
As an example of MTI randomization, suppose there is a trial in which participants are randomized into one of two arms: treatment or placebo. The investigator for this trial chose an MTI value = 3. Consequently, as participants are randomized, the imbalance between the number of participants assigned to treatment and the number assigned to placebo will never exceed 3 participants.
Suppose this trial is about to randomize its 8th participant. Among the first 7 participants randomized, 4 went to the treatment arm and 3 to placebo. This next participant has the possibility of being assigned to either treatment or placebo (in other words, the 8th allocation is NOT deterministic), because in either scenario the imbalance between the arms will not exceed 3 participants.
However, suppose among the first 7 participants randomized, 5 went to the treatment arm and 2 to placebo. Since the imbalance is currently at three, the next participant must go to placebo. An assignment to the treatment arm would create an imbalance of 4 participants, which is not allowed, as the investigator selected an MTI value = 3.
Choice of MTI value
The choice of the MTI value will determine how imbalanced the arms can ever become. A small MTI value will maintain tight arm balance but suffer from increased predictability of arm assignment. Conversely, a larger MTI value increases randomness but is susceptible to greater arm imbalance. For large trials, a larger MTI value may be appropriate, and small trials might employ a smaller MTI value. The choice of the MTI value is up to the investigator. If you are using the randomization tool on this site, a default MTI value is provided.
Choice of randomization procedure
A variety of MTI procedures are available. Each follows its own algorithm to calculate the randomization sequence, but they all determine the probability of participant allocation to treatment arms based on the imbalance in treatment arm assignment up to that point in time.
Among the MTI procedures are: the maximal procedure [2], the asymptotic maximal procedure [3], the big stick procedure [4], Chen's procedure [5], and the block urn design [6]. Table II of [7] provides a comparison of available MTI procedures. The choice of procedure is up to the investigator. If you are using the randomization tool on this site, the default procedure is the asymptotic maximal procedure.
For all of the following MTI procedures (and indeed for any MTI procedure), arm balance is maintained by the MTI value, as described above. If the difference between the numbers of participants assigned to any two arms ever reaches the MTI value, the next allocation is deterministic and forces an allocation in the direction of arm balance. Therefore, arm imbalances can never exceed the MTI value.
Maximal procedure
Among MTI procedures, the maximal procedure is an excellent option for reducing the overall predictability of treatment assignment. This is achieved, in concept, by constructing all possible randomization sequences constrained by the MTI value, and then selecting one of these allocation sequences at random. Therefore, each possible allocation sequence is equally likely. In the resultant randomization sequence, the probability of assignment to each arm will depend on (1) the current imbalance between arms and (2) the number of participants that have been randomized (i.e., the current location within the randomization sequence).
In the maximal procedure (and the related asymptotic maximal procedure, discussed next), if the arm sizes become more unbalanced, greater balance-forcing probabilities are encountered. Conversely, as the arms become more balanced, arm assignments become more random.
Asymptotic maximal procedure
The asymptotic maximal procedure is based upon the same principles as the maximal procedure but is simpler in design and implementation. In the asymptotic maximal procedure, the probability of arm assignment depends only on the size of the imbalance between the arms. This differs from the standard maximal procedure, in that the asymptotic maximal procedure does NOT consider the location within the randomization sequence.
As the trial size increases, the asymptotic maximal procedure becomes more and more similar to the standard maximal procedure.
Chen's procedure
Like the maximal and asymptotic maximal procedures, Chen's procedure applies a balance-forcing probability when the current arm sizes are unbalanced. Unlike the maximal and asymptotic maximal procedures, this balance-forcing probability is a constant value, which the user specifies. In other words, Chen's procedure ignores the extent of imbalance (at least until the MTI value is reached) and considers only whether arms are or are not balanced.
Big stick procedure
The big stick procedure is the simplest of the MTI procedures. Arm imbalances are constrained only by the MTI value. For any imbalance within the MTI value, no balance-forcing probability is applied. There is equal allocation until the MTI value is reached.
Block urn design
Another method is the block urn design, which in some ways is analogous to permuted blocks (see Other Non-MTI Randomization Methods below), but much improved in that the blocks "reset" under certain conditions, thereby reducing the overall predictability of arm assignments.
As previously mentioned, not all randomization procedures are equally random. Some are more susceptible to selection bias, and others to unacceptable levels of imbalance in treatment assignments. The examples in this section for non-MTI methods are not recommended; they are shown only for comparison.
In contrast to non-MTI randomization methods, the MTI randomization procedures previously shown on this page provide a better combination of randomness of assignment and balanced treatment arms.
Unrestricted randomization
In concept, unrestricted randomization is like tossing a fair coin for each participant assignment. The most apparent concern with unrestricted randomization is the risk of large treatment arm imbalances after all participants have been assigned. A related concern is chronological bias [8]. Chronological bias occurs when one treatment is assigned too frequently or infrequently within given periods of time, and is a problem if the timing of treatment assignment influences the treatment result (i.e., time becomes a confounding variable for treatment assignment and result). Moreover, it is impractical to use unrestricted randomization in the way intended [9].
Permuted block randomization
Many researchers are aware of a method called permuted block randomization. As the name suggests, treatment arm assignment order is arranged within small blocks. By the end of each block, an exact number of participants have been assigned to each treatment arm; a researcher could know with certainty the treatment arm assignments for the last participant(s) in a block. A clear disadvantage to permuted block randomization is high arm assignment predictability and, therefore, susceptibility to selection bias. Block randomization is not preferred, given that better methods are available [10].
Why MTI procedures are preferred to non-MTI methods
The randomization process should aim to reduce the predictability of treatment assignment while maintaining balance of treatment over time.
In comparison to MTI randomization, non-MTI approaches are not recommended as they are either too predictable or too imbalanced. Although permuted block randomization is frequently employed, this approach is significantly less random than comparable MTI procedures. Meanwhile, unrestricted randomization has no means of maintaining balance between the treatment arms.
MTI randomization methods preserve balance between treatment arms while achieving a greater degree of randomness at each allocation. The randomization tool on this site offers a variety of MTI randomization methods to generate randomized allocation sequences for use in clinical trials.
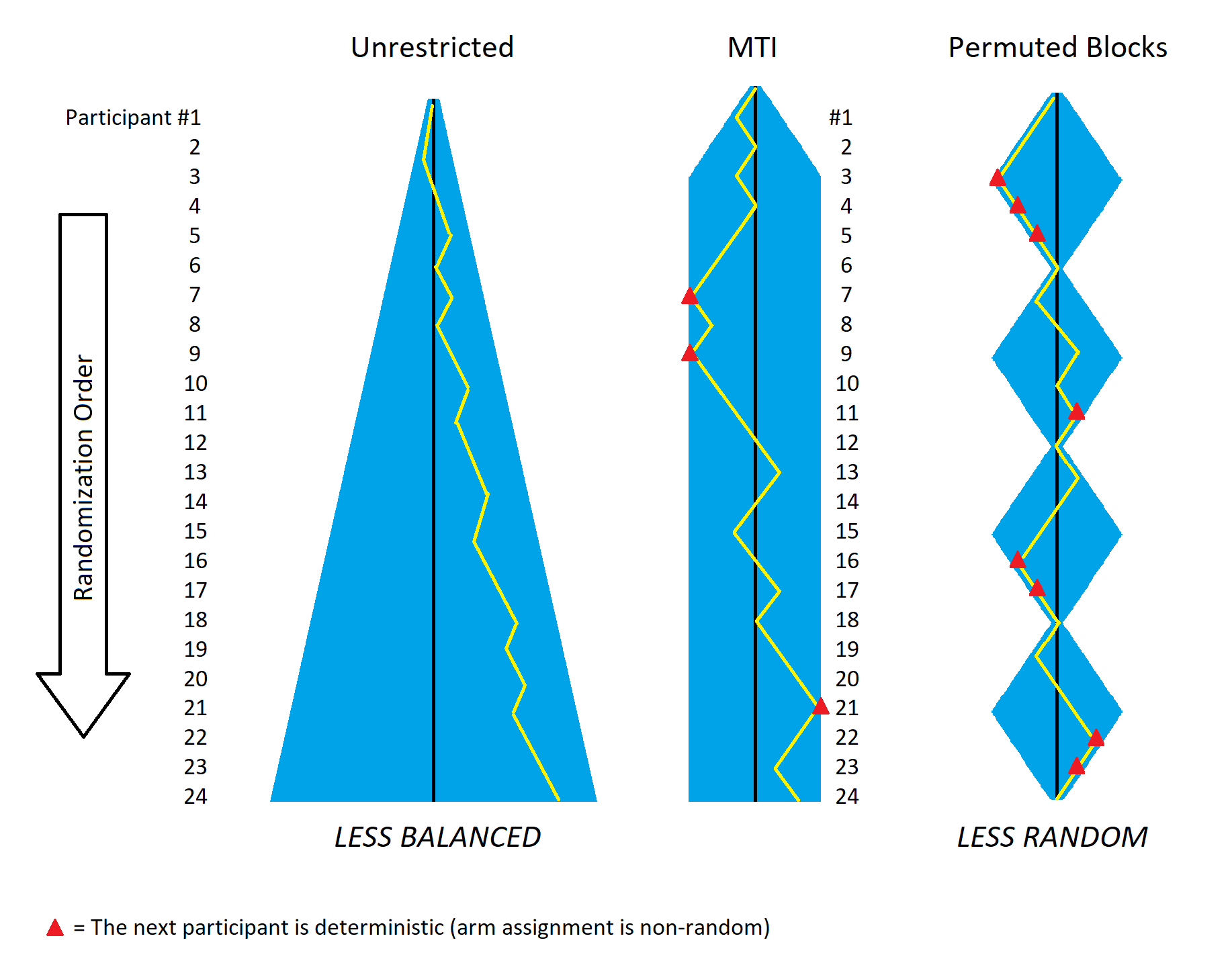
Three distinct trials using: unrestricted randomization (left panel); MTI randomization (central panel); and permuted blocks (right panel). The blue shaded areas represent possible arm imbalances in each approach, and the yellow lines track the arm imbalance for a hypothetical trial of 24 participants.
MTI randomization (center) offers a good middle ground between balance and randomness. Balance between arms in unrestricted randomization (left) isn't enforced. By contrast, block randomization (right) forces arms back to balance too frequently, reducing randomness and yielding more predictable arm assignments. In this example with fixed block size of 6, each block has at least 1 and as many as 3 deterministic allocations (red triangles). Even when variable block sizes are employed, the forced return to balance is so frequent that the overall predictability is notably higher than comparable MTI methods.
- Berger VW. Senn S, Barnett V, Berger VW, eds. Selection Bias and Covariate Imbalances in Randomized Clinical Trials. John Wiley & Sons, Ltd.; 2005. doi:10.1002/0470863641
- Berger VW, Ivanova A, Deloria-Knoll M. Minimizing Predictability while Retaining Balance through the Use of Less Restrictive Randomization Procedures. Statistics in Medicine. 2003;22(19):3017-3028. doi:10.1002/sim.1538
- Zhao W, Berger VW, Yu Z. The Asymptotic Maximal Procedure for Subject Randomization in Clinical Trials. Statistical Methods in Medical Research. 2018;27(7):2142-2153. doi:10.1177/0962280216677107
- Soares JF, We CFL. Some Restricted Randomization Rules in Sequential Designs. Communications in Statistics Theory and Methods. 1983;12:2017-2034. doi:10.1080/03610928308828586
- Chen YP. Biased Coin Design With Imbalance Intolerance. Communications in Statistics Stochastic Models. 1999;15:953-975. doi:10.1080/15326349908807570
- Zhao W, Weng Y. Block Urn Design -- A New Randomization Algorithm for Sequential Trials with Two or More Treatments and Balanced or Unbalanced Allocation. Contemporary Clinical Trials. 2011;32(6):953-961. doi:10.1016/j.cct.2011.08.004
- Berger VW, Bejleri K, Agnor R. Comparing MTI Randomization Procedures To Blocked Randomization. Statistics In Medicine. 2016;35:685-694. doi:10.1002/sim.6637
- Matts JP, McHugh RB. Conditional Markov Chain Design for Accrual Clinical Trials. Biometrical Journal. 1983;25:563-577. doi:10.1002/bimj.19830250608
- Berger VW. The Alleged Benefits of Unrestricted Randomization. In: Berger VW, ed. Randomization, Masking, and Allocation Concealment. CRC Press, Chapman and Hall; 2018. doi:10.1201/9781315305110
- Berger VW. Allocation Concealment and Blinding: When Ignorance is Bliss. Medical Journal of Australia. 2005;183(3):165. doi:10.5694/j.1326-5377.2005.tb06974.x
